|
Selection Bias in Genetic Algorithms
In genetic algorithms, members of a population are selected for reproduction.
Selection Bias - Implementation of the idea that stronger chromosomes should be selected for reproduction more often than weaker chromosomes.
There's two basic ways to implement selection bias. Well, actually 3, but I'm not a big fan of tournament selection.
Roulette Wheel - Imagine that we have 10 chromosomes with fitness values between 1 and 10. Step one: Add each chromosome to the roulette wheels such that the chromosomes with higher fitness have a bigger "slice of the pie"
For the following chromosome fitness values:
| Chromo: |
A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
| Fitness: |
5 |
2 |
3 |
1 |
6 |
4 |
9 |
10 |
3 |
4 |
This pie chart shows Chromosomes with corresponding fitness values and selection biases. The bias is represented as a percentage and refers to a chromosome's chance of being selected for the parent pool for each pick from the population.
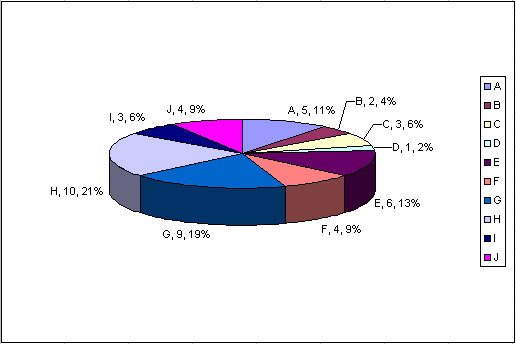
Figure: Chromo, Fitness, Selection %
|
Rank Selection
Rank selection is very straight forward. To be honest, it is Roulette wheel with a presort. To begin, chromosomes are sorted in order of highest fitness to lowest fitness with the highest being awarded a rank of 10 (since our population size is 10). The higher the rank, the higher the fitness.
Yes, I know it makes sense to give the highest fitness a rank of 1, but doing it my way saves us a step. You'll see why shortly. After the sort is complete, a roulette wheel is built based upon the rank instead of fitness. For the same bunch of chromosomes above, here's the new pie chart:
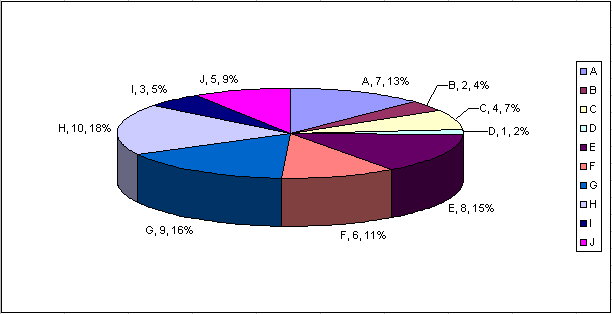
Figure: Chromo, Rank, Selection %
As a rule of thumb, rank selection allows average-fitness chromosomes to do a bit more breeding. I've not had much success with this particular selection method, but others have. Like everything else in genetic algorithms, it's problem dependent. So, it's worth implementing and testing out to see if it works for your project.
|
Roulette Wheel - How do I code this thing?
It's a little tricky, but easy to implement once you get the idea.
What I like to do is build an array of integers or floating points, whatever the datatype of the fitness value is. For the first spot in the array, insert the fitness value of the first chromosome. For the second spot, input the fitness value of the second chromosome PLUS the fitness value of the first chromosome. The third is the combined fitness of the first three chromos, and so on. Also, it's a good idea to store the combined fitness of all chromos in a variable named Total.
Once the array is built, get your randomizer ready. Select a random number between 0 and the Total variable. Now, perform a binary search through your array. The idea: take the index of the first number in the array that is greater than the random number you generated. This number is the index of the chromosome to put in the parent pool.
If this went over your head, think of it as a number line with notches at certain intervals that represents different fitness values (or size of pie slices!). When you generate a random number, it falls somewhere on the number line. So, you have to write some code to determine where on the number line it fell, and return the number that represents that part of the number line (or the the pie slice!). If binary searches aren't your thing, feel free to use other search methods. Brute force will be OK if your population size isn't too big.
If you're still having trouble grasping this, get a piece of paper out and draw a fake population of chromosomes with fitness values. Draw a number line and pie chart, and then design an algorithm to simulate selection from the number line or pie chart.
|